Optimizing Query Evaluations using Reinforcement Learning for Web Search
As part of my research at Microsoft Bing, we developed a novel algorithm to search a very large index for documents related to a query. Rather than scanning the index for matching terms using hand-crafted rules, we propose a reinforcement learning approach that seeks to optimize the tradeoff between finding important documents and computation time. Please see our preprint on Arxiv which was accepted to Sigir 2018 in July.
Knowledge Base Completion with Embeddings of Graphs, Text, and Paths
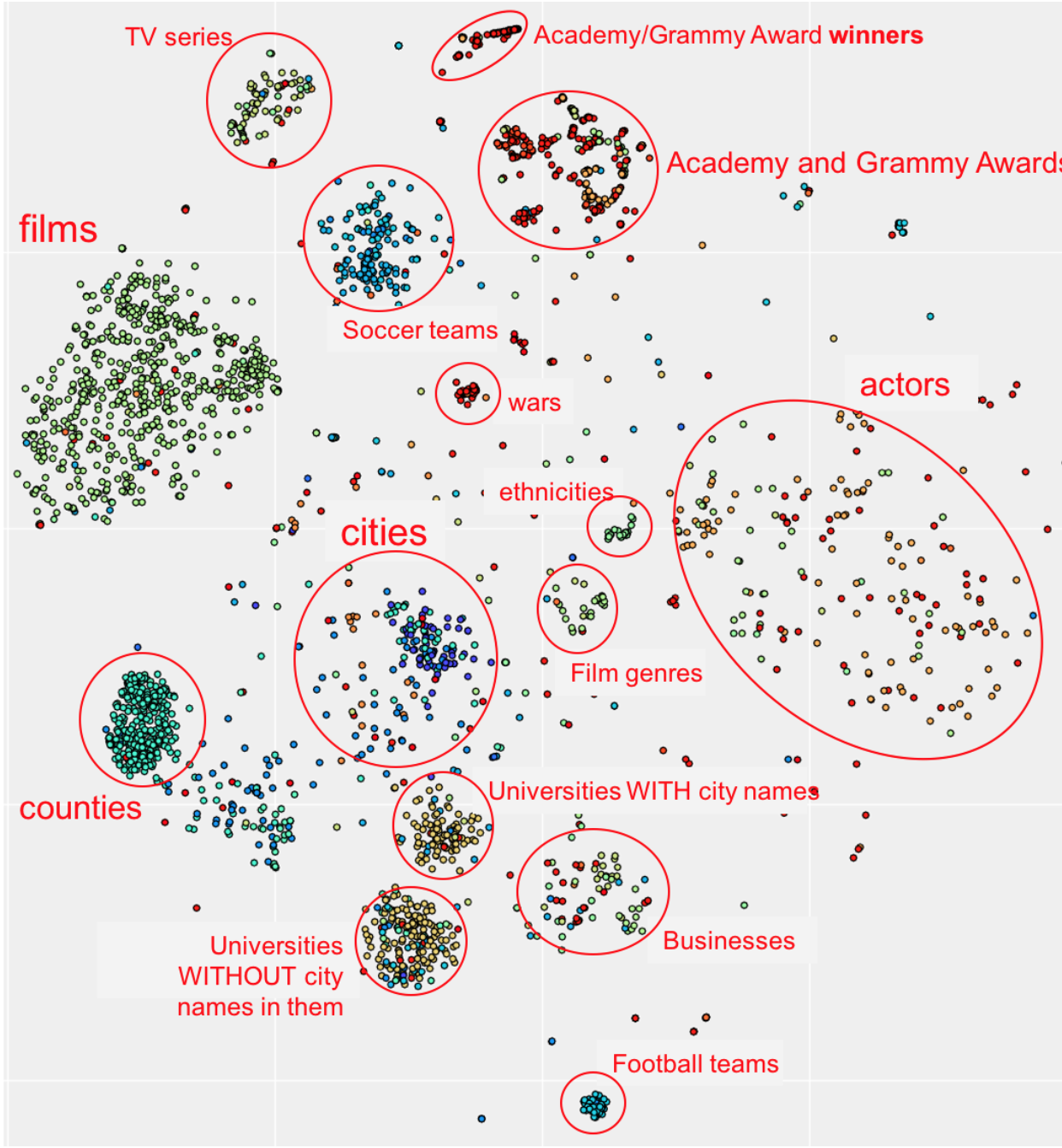
This is research I conducted as part of a Senior Honors Thesis for the Computer Science Department with the generous support of the Pistritto Fellowship. I worked on algorithms for learning entity and relation-specific embeddings of knowledge graphs, and different training approaches for the task of knowledge graph completion. The abstract is here:
Knowledge bases are an effective tool for structuring and accessing large amounts of multi-relational data, but they are often woefully incomplete, especially in broader domains. We consider the task of learning low dimensional embeddings for Knowledge Base Completion and make the following contributions: 1) a novel embedding model, ModelE-X, that uses few parameters yet outperforms many state-of-the-art, more complex algorithms, 2) the realization that the often-unreported metric of relation ranking yields valuable insights into algorithms' behavior and 3) we scrutinize macro vs. micro-averaging of ranking metrics and discuss which is a better indicator of generalizability.
Deep Canonically Correlated LSTMs
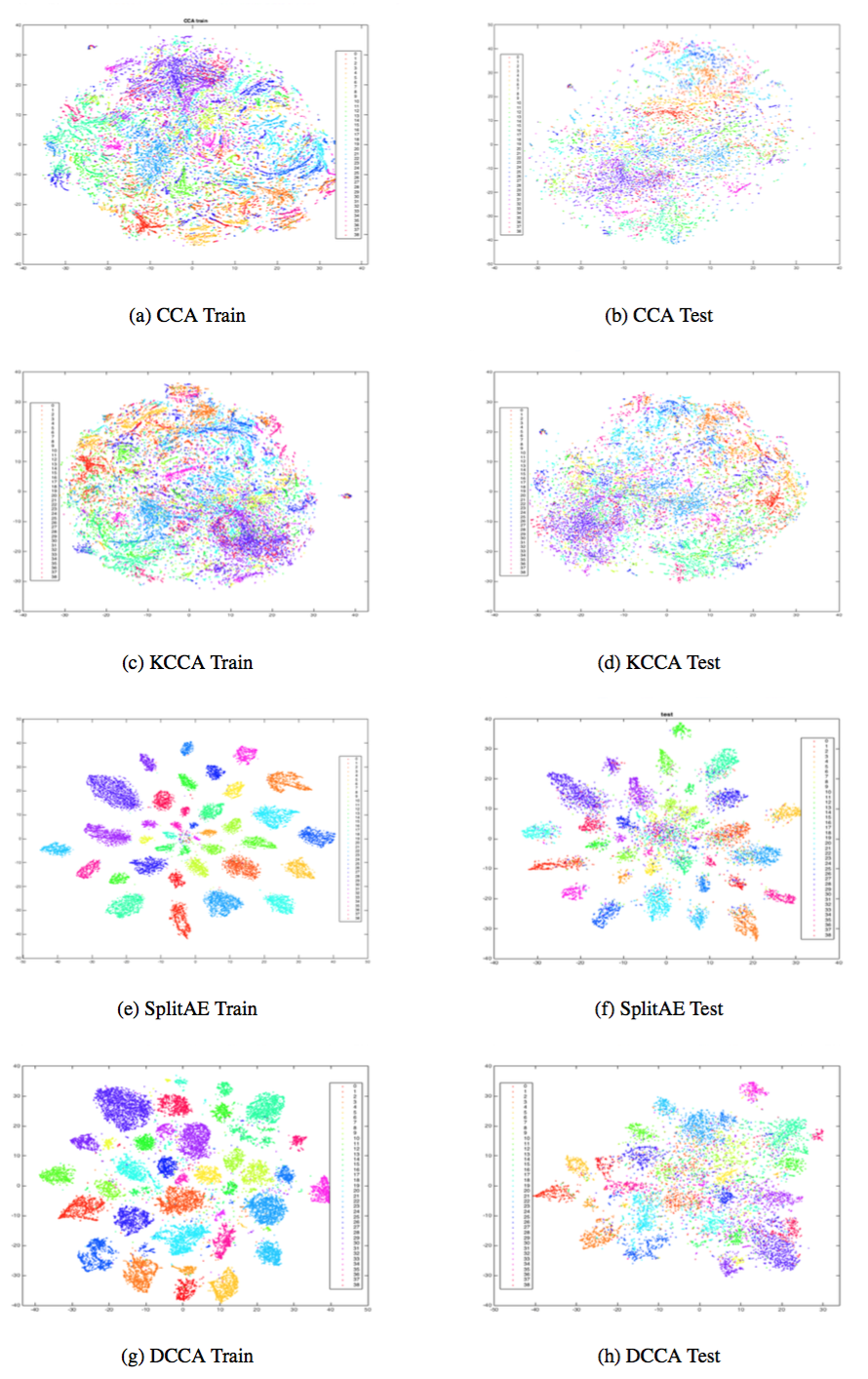
This was a research project with my colleague Neil Mallinar for his Thesis at Johns Hopkins University. We wanted to investigate whether the CCA objective could be used in time series settings. The abstract is here:
We examine Deep Canonically Correlated LSTMs as a way to learn nonlinear transformations of variable length sequences and embed them into a correlated, fixed dimensional space. We use LSTMs to transform multi-view time-series data non-linearly while learning temporal relationships within the data. We then perform correlation analysis on the outputs of these neural networks to find a correlated subspace through which we get our final representation via projection. This work follows from previous work done on Deep Canonical Correlation (DCCA), in which deep feed-forward neural networks were used to learn nonlinear transformations of data while maximizing correlation.